黄色小电影 基于集成优化的感应电机无权重悉数接洽转矩规则
纲目 接洽转矩规则行为一种新兴的规则战略，通过计较主张函数中的转矩与磁链短处，中式最优开关现象，频年来被粗犷期骗于交流调速电机系统。与传统的矢量规则比较，接洽转矩规则具有动态反馈快、开关频率低等上风。为谐和主张函数中不同短处项的量纲，接洽转矩规则需要想象悉数用于调遣转矩与磁链短处的权重。然则，依据教化想象的权重悉数难以相宜不同工况要求。针对以上问题，该文提议一种基于集成优化结构的无权重悉数接洽转矩规则战略。该规则战略同期优化转矩与磁链短处项，分别得到3个转矩最优与磁链最优的开关现象序列，通过集成优化算法求解最优开关现象。实验收场标明，基于集成优化的无权重悉数接洽转矩规则在多种工况下具备较好的稳态与动态性能。
要害词：感应电机 接洽转矩规则 无权重悉数 集成优化
0 小序频年来，模子接洽规则以其结构浅显、易于处理敛迹优化及多变量非线性规则系统问题等优点，迟缓成为期骗于电力电子变换器与电机驱动的新兴规则要领[1-3]。与传统矢量规则要领比较，模子接洽规则进行调制，不错获取更快的动态反馈特色[4-5]。跟着数字信号处理器及现场可裁剪门阵列的马上发展，对计较材干的尖酸要求将不再是模子接洽规则的绝交与挑战[6-7]。因此，模子接洽规则在电机驱动场地具有更粗犷的期骗远景[8-14]。
接洽到逆变器开关现象的破碎特色，行为模子接洽规则的一个蹙迫分支，有限集模子接洽规则可用于规则电机驱动系统[15-16]。从数学优化角度来看，该规则战略以系统模子与决议变量来接洽系统的改日现象，构造相应的主张函数，以主张函数最优为依据中式开关现象[17]。把柄规则变量来分别，有限集模子接洽规则不错分为接洽转矩规则、接洽电流规则、接洽速率规则等[18-19]。其中，接洽电流规则以定子电流行为规则变量，而接洽转矩规则以减小转矩与定子磁链短处行为规则主张，将求解主张函数最小值行为二次贪图问题，中式逆变器的最优开关现象[20]。
国表里学者对接洽转矩规则进行了深远粗犷的究诘。文件[21]提议了一种基于区域电压矢量表的交流异步电动机转矩接洽规则战略。该要领在区域电压矢量表的基础上接洽转矩与磁链，进一步裁减转矩脉动，提高了系统的稳态性能。文件[22]提议了一种基于永磁同步电机的接洽转矩规则要领，与传统平直转矩规则要领比较，治理了转矩与定子磁链脉动较大的问题。然则，该规则战略需要出奇引入权重悉数调遣不同运作事态下的评估收场。文件[23]禁受基于开关表的纠正型模子接洽规则战略，用于规则三电平逆变器永磁同步电机。该纠正战略在竣事对中点电位、转矩及磁链规则的基础上，进一步减小了模子接洽规则的计较量。文件[24]深远推导了磁链与转矩的认识关系，将电磁转矩与定子磁链鼎新为等效定子磁链进行规则。实验收场标明，基于等效磁链的感应电机模子接洽规则要领在较宽使命边界具有精好意思性能。
然则，权重悉数的想象与优化仍然是接洽转矩规则亟待治理的问题。针对这一问题主要有以下三种念念路：权重悉数在线修正[25]、离线神经网罗调 节[26]、权重悉数舍弃等[27-29]。文件[25]提议了一种权重悉数调遣的代数想象依据，在给定的开关频率下，以最小电流总谐波失真为依据求解最优权重悉数。该要领仅接洽了开关频率与电流总谐波失竟然关系，未对权重悉数在不同工况下的影响进行分析。天然给出了权重悉数的想象依据，但本色上仍然依赖权重悉数对老本函数中的不同规则变量短处项进行调遣。文件[26]提议了一种禁受东谈主工神经网罗对基于电力电子变换器的模子接洽规则权重悉数的想象要领。然则，神经网罗要领依赖多数数据，存在计较量较大的颓势。此外，该要领雷同未舍弃权重悉数。文件[27]提议了一种浅显的串联接构模子接洽规则战略。为了舍弃权重悉数，该规则要领将主张函数解析为两个单一规则变量的短处多项式，以级联接构循序优化。然则，该要领的局限性在于无法保证中式全局最优解。由于优化转矩短处中式的开关矢量较少，存在磁链及电流规则后果较差的问题。文件[28]通过谐和接洽模子的现象变量，提议了一种基于两电机转矩同步系统的有限集模子接洽规则要领。然则，该要领依赖同步电流短处，局限于两电机同步系统，需要为电流追踪短处项与同步短处项想象出奇的权重悉数。为舍弃权重悉数，文件[29]提议了一种三矢量模子接洽转矩规则要领。该要领的价值函数中只包含转矩这一规则变量，并禁受无差拍规则时代计较出各矢量的作用时期。但是，该要领对模子参数精度较为敏锐。此外，在疏通的采样频率下，多矢量模子接洽规则在一个采样周期内可能履行多个开关矢量，具有较高的开关频率。
针对模子接洽规则中的多规则主张决议问题，学者们引入了集成优化过火关连见识。文件[30]提议了一种基于模子接洽规则的动态多属性决议要领。文件[31]提议了一种以名次行为遴荐依据无权重悉数接洽转矩规则要领。然则，该要领为均衡转矩及磁链名次函数的影响，引入了出奇悉数。文件[32]提议了一种基于感应电机的谐和化多矢量模子接洽规则。该要领禁受无差拍时代与调制战略平直获取合成矢量过火占空比，揭示了多矢量模子接洽规则与空间矢量调制战略的关系。
本文提议了一种基于集成优化的感应电机接洽转矩规则要领。为舍弃权重悉数的影响，该规则要领的主张函数被解析成具有单一规则变量的转矩短处项与磁链短处项。对转矩与磁链短处项同期进行优化，分别得到3个较优的开关现象。随后，对两组较优的开关现象进行集成优化，求解出全局最优解，用于规则逆变器的开关现象。通过实验收场讲授了所提议规则要领的可行性，与传统接洽转矩规则比较，具有较好的稳态与动态性能。
1 系统模子本文以笼型感应电机及三相两电平逆变器构建系统模子。感应电机的数学模子可暗示为
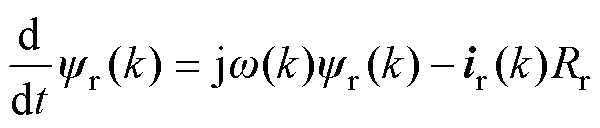（2）
其算计定子与转子磁链为
（4）
式中，Rs、Rr分别为定子、转子等效电阻；Ls、Lr、Lm分别为定子电感、转子电感、互感；is、ir分别为定子、转子电流；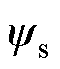
、
分别为定子、转子磁链；w 为转子转速；vs为电压矢量，由两电平逆变器产生。
两电平三相逆变器过火开关现象如图1所示。当两电平逆变器上桥臂开关管导通时，该相电压为直流母线电压uDC。禁受Clarke变换，有
usab=Kusabc （5）
其中
式中，K为Clarke变换矩阵；usab 为ab 正交坐标系下的定子电压；usabc为三相静止坐标系下的定子电压。
2 基于集成优化的无权重悉数接洽转矩规则要领为舍弃权重悉数对接洽转矩规则性能影响，本文在简要先容传统及串联接构接洽转矩规则的基础上，提议了一种基于集成优化的无权重悉数接洽转矩规则要领。该要领主要包括规则变量接洽、主张函数想象、延时抵偿及集成优化算法等部分。
2.1 接洽转矩规则在接洽转矩规则要领中，最初需要对转矩T及定子磁链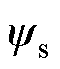这两个规则变量进行接洽。以Ts行为采样周期，把柄感应电机数学模子及欧拉破碎公式，定子磁链及定子电流的接洽值可暗示为
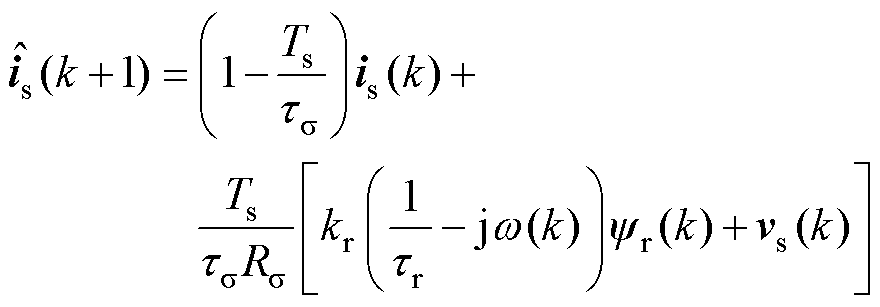（7）
其中
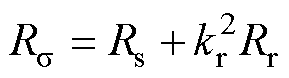
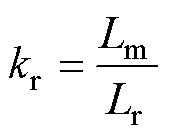
式中，s 为漏感悉数。
电磁转矩接洽值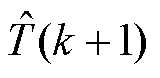
可由定子磁链与定子电流的接洽值
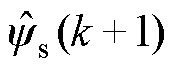及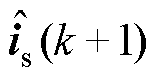
计较得出，有
式中，p为电机极对数。
由于接洽转矩规则的规则主张是减小定子磁链和转矩接洽值与其参考值的短处。因此，接洽转矩规则的主张函数gj界说如式（9）所示，用于求解该包含出奇敛迹的二次贪图问题。
式中，定子磁链的基准值
为额定值；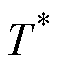
为转矩基准值，由所测速率与速率基准值的短处经过速率
PI环给出。为调遣转矩与磁链短处对求解主张函数极值的影响，引入权重悉数l 以谐和两个短处项的量纲。当N配置为2时，该规则要领为接洽延时抵偿的单步长接洽转矩规则。Im(k+h)为竣事电流收尾的出奇敛迹，当is(k+h)＜ismax时，Im(k+h)=0；反之Im(k+h)为正无尽。接洽转矩规则框图如图2所示。
2.2 基于集成优化的无权重悉数接洽转矩规则天然传统模子接洽规则的主张函数不错同期竣事减小转矩与磁链短处，但是其主张函数包括多个规则变量，教化得出的固定权重悉数无法针对不同工况下的主张函数求解作出优化。为克服以上颓势，本文提议了一种基于集成优化的无权重悉数接洽转矩规则要领。该规则战略将传统接洽转矩规则中的多规则变量主张函数解析为两个单一规则变量的短处项gTj、gFj并同期优化，分别得到转矩较优与磁链较优的开关现象序列VT与VF，以集成优化的样式获取共同开关现象，以舍弃权重悉数的不利影响。值得精细的是，电流收尾敛迹Im(k+h)分别期骗于gTj与gFj中，有
最初，遍历两电平逆变器的通盘开关现象（j= 0～6），通过计较并比较转矩、磁链短处项gTj及gFj值，遴荐转矩较优与磁链较优的开关现象序列。对应转矩短处项gTj较小的3个开关矢量jT1、jT2与jT3寄存在转矩较优的开关现象序列VT中，相应地，对应磁链短处项gFj较小的3个开关现象jF1、jF2与jF3寄存在转矩较优的开关现象序列VF中。将VT与VF中的开关现象禁受集成算法优化，得到最终所需的最优开关现象。
由于在接洽转矩规则中，转矩接洽值的计较受磁链接洽值影响。因此，减小转矩短处项具有较高的优先级。若VT与VF中存在疏通的开关现象，则在共同开关现象中使转矩短处项gTj最小的开关现象行为最优解。若VT与VF中不存在疏通的开关现象，则界说不属于VF的开关现象为磁链次优解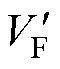
。此时，遴荐VT与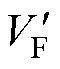中存在疏通的开关现象，若存在多个共同开关现象，其中使磁链短处项gFj最小的开关现象行为最优解。最终，将所得最优解输出至逆变器中规则感应电机运行。因此，基于集成优化的无权重悉数接洽转矩规则框图如图3所示。
基于集成优化的无权重悉数接洽转矩规则过程如图4所示。该算法枢纽描写如下：
（1）系统驱动化，驱动化开关现象的寄存序列VT、VF，测量转速与电流。
（2）估算定子与转子磁链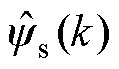
、
。
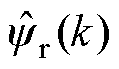（3）计较定子电流、定子磁链与转矩的接洽值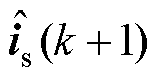
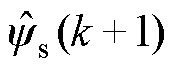、与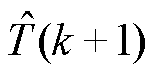
，接洽延时抵偿的接洽值
、
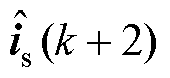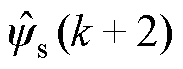与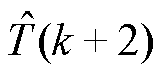
。
（4）遍历通盘开关现象for j=0～6，分别将转矩最优与磁链最优的3个开关现象寄存在VT与VF中。
（5）将VT与VF中的开关现象通过集成优化算法，求解全局最优的开关现象，输出到逆变器中。
为进一步报告基于集成优化的无权重悉数接洽转矩规则战略的优化旨趣，以文件[25]为实例具体诠释。表1把柄gT(vs)与gF(vs)的值，转矩较优的3个开关矢量循序为v0、v5、v3，磁链较优的3个开关矢量循序为v3、v2、v1。通过集成优化算法，转矩短处最小的共同矢量为v3。
表1 基于集成优化的接洽转矩规则开关矢量遴荐实例1
表2所示为本文所述算法可能出现的少许数情况，转矩较优与磁链较优的3个开关矢量无共同矢量。此时，转矩较优的3个开关矢量循序为v0、v5、v3，磁链较优的3个开关矢量循序为v4、v2、v1，转矩次优的4个开关矢量循序为v0、v6、v5、v3。在转矩较优的3个开关矢量与转矩次优的4个开关矢量中遴荐磁链短处最小的共同矢量，为v0。
表2 基于集成优化的接洽转矩规则开关矢量遴荐实例2黄色小电影
3 实验考据为考据本文提议的基于集成优化的无权重悉数接洽转矩规则，搭建如图5所示的实验平台。该实验平台由两台2.2kW笼型感应电机及基于Linux系统的1.4GHz及时规则系统组成。主电机由3.0kW Danfoss逆变器驱动，负载电机由基于IGBT的14kV·A Servostar变频器驱动。用于比较的两种规则战略所禁受的开关频率均为16kHz，传统接洽转矩规则的权重悉数为10。同期，在采样频率为10kHz的测试要求下，给出了两种规则战略在N=3的多步长要求下的对比分析。实验平台组成见表3，感应电机参数见表4。
最初通过实验对两种规则战略的稳态性能进行对比分析。图6a为本文提议的基于集成优化的无权重悉数接洽转矩规则要领；图6b为传统接洽转矩规则要领。从图中不错看出，两种规则战略均使命在转速为1 910r/min、转矩为4N·m、N=2的稳态要求下。由于无权重悉数要领通过集成优化竣事了权重悉数的调遣，与传统接洽转矩规则比较，其转矩与磁链短处脉动分别减小了32%和25%（Tripple=1.5N·m， ysripple= 0.06Wb），并获取了较好的定子电流质地（isTHD= 7.5%）。两种规则要领的稳态收场比较见表5。
表3 各部分实验平台组成
表4 感应电机参数
图7所示为N=3时的多步长传统接洽转矩规则与基于集成优化的无权重悉数接洽转矩规则稳态性能对比分析。两种多步长接洽转矩规则禁受的采样频率为10kHz，转速为1 910r/min，转矩为4N·m。从图7a不错看出，基于集成优化的无权重悉数接洽转矩规则具有较小的转矩脉动及电流总谐波畸变率（Total Harmonic Distortion， THD），分别为1.4N·m及9.9%。与多步长传统接洽转矩规则比较，转矩脉动及电流THD分别减少了44%及33%。由此不错看出，基于集成优化的权重悉数舍弃要领关于多步长接洽转矩规则的规则后果具有较彰着普及。
表5 两种规则要领稳态收场比较
图8为N=2时两种规则战略在额定转速回转使命要求下的实验收场。从图8a中不错看出，所提议的集成优化无权重悉数接洽转矩规则要领唐突竣事在全转速边界内运行，并具有较好的动态反馈特色。在t =0.92s时刻转速从2 772r/min下落至-2 772r/min，转速回转过程用时为0.28s。关于传统接洽转矩规则，该过程时期为0.32s。由于两种规则战略禁受了疏通的速率环PI参数，故均具有较快动态反馈。转速回转过程中，本文所提规则战略的转矩短处脉动为Tripple=1.8N·m，磁链短处脉动ysripple=0.06Wb。
通过实验考据所提议的无权重悉数接洽转矩规则的瞬态规则性能。图9所示为N=2时该规则算法的转矩扰动实验收场，自上而下循序为转速、转矩、三相定子电流及定子磁链波形。感应电机运行在转速为100rad/s的工况下，驱动无负载转矩。在转矩扰动瞬态，通过规则表盘提供5N·m的转矩扰动，转速从955r/min裁减至820r/min，并在120ms内回到原始值。图10为放大转矩波形，不错看出，转矩在90ms内从0N·m增多到5N·m。实验收场讲授，基于集成优化的无权重悉数接洽转矩规则具有较好的瞬态规则性能。
图11给出了两种N=3的多步长接洽转矩规则战略转矩扰动实验的对比收场，转速为955r/min，转矩扰动为5N·m。不错看出，两种要领均具有较快的动态反馈特色。由于禁受疏通的PI参数，两种要领具有相似的转速规复时期与转矩高潮时期。集成优化无权重悉数接洽转矩规则的转速规复时期约为130ms，转矩高潮时期为33ms。传统接洽转矩规则的转速规复时期约为120ms，转矩高潮时期约为45ms。与传统接洽转矩规则要领比较，基于集成优化的无权重悉数接洽转矩规则的转矩及磁链脉动减少了34%与21%，分别为1.4N·m与0.055Wb。
小色尼姑庵图12给出了N=2时两种规则战略的转矩阶跃实验对比分析。感应电机转速为480r/min，转矩基准值为3N·m，定磁链基准值为0.71Wb。当转矩阶跃时，转矩基准值从3N·m阶跃至5N·m。与此同期，转速从480r/min高潮至625r/min（增多了30%），经过约450ms回到驱动值。由于两种规则战略禁受了疏通的PI参数，因此具有相似的动态反馈后果。该无权重悉数接洽转矩规则的转矩短处脉动Tripple与磁链短处脉动ysripple分别为1.8N·m与0.06Wb，isTHD约为8.0%。
图13给出了N=3的基于集成优化的无权重悉数接洽转矩规则与传统接洽转矩规则转矩阶跃实验收场。对比实验的使命要求与两种规则要领在N=2时一致。从图13a中不错看出，基于集成优化的无权重悉数接洽转矩规则要领的转矩脉动为1.3N·m，磁链短处为7%，电流THD=9.1%。图13b所示的传统接洽转矩规则的规则后果参数分别为1.7N·m、7%及9.8%。与N=2时的对比收场一致，基于集成优化的无权重悉数接洽转矩规则具有较小的转矩脉动、磁链短处脉动及定子电流THD。
图14给出了N=2的基于集成优化的无权重悉数接洽转矩规则与传统要领的磁链阶跃规则后果对比分析。从图中不错看出，感应电机转速为480r/min且无负载转矩，定磁链基准值从0.71Wb增多到0.91Wb。与传统接洽转矩规则比较，该无权重悉数要领在磁链阶跃之后，保捏了较踏实的转速，其脉动减小了30%（46r/min），转矩短处脉动与磁链短处脉动分别为1.9N·m与0.08Wb。
图15给出了N=3的两种规则要领磁链阶跃实验收场。当磁链基准值增多至0.91Wb时，两种要领的转矩短处均有所增大。如图15a所示，磁链阶跃后基于集成优化的无权重悉数接洽转矩规则转速脉动为35r/min，转矩脉动为1.1N·m。与传统接洽转矩规则比较，转速与转矩脉动分别减少了36%与45%。
图16给出了基于集成优化的无权重悉数接洽转矩规则对参数失配鲁棒性实验收场。感应电机运行在300r/min且无负载转矩的工况下。图16a为定子电阻失配鲁棒性测试，定子电阻在0.13s内从额定值2.68W 变化至3.8W（失配为41.7%）。从图16a中不错看出，基于集成优化的无权重悉数接洽转矩规则运行较为踏实，转速、转矩均无彰着颠簸（仅为10r/min及0.1N·m）。因此，该规则要领能承受约40%的定子电阻失配。图16b为转子电阻失配鲁棒性测试，转子电阻从额定值2.13W 变化至3.8W（失配为78.4%）。与定子电阻失配比较，该规则要领对转子电阻失配具有更好的鲁棒性，险些无转速及转矩颠簸。
（a）定子电阻Rs从2.68W 增多至3.8W
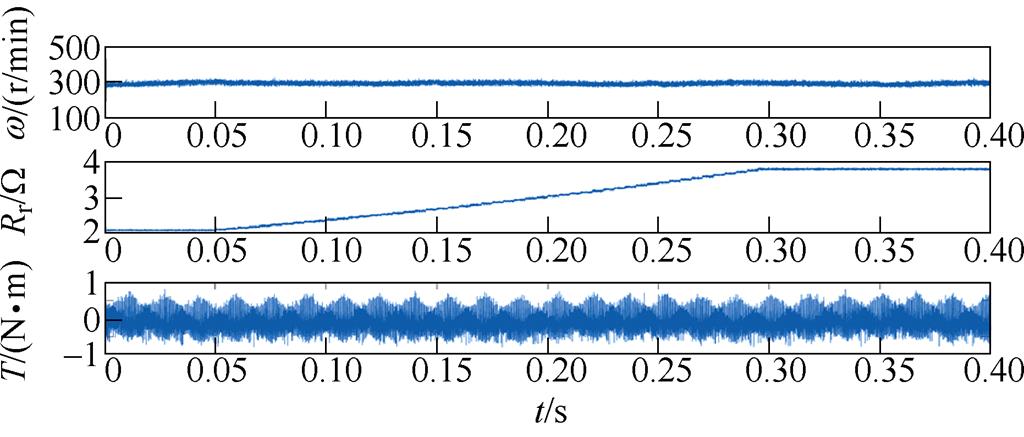
（b）转子电阻Rr从2.13W 增多至3.8W
图16 基于集成优化的无权重悉数接洽转矩规则参数鲁棒性实验收场（w =300r/min， T=0N·m， N=2）
Fig.16 Robustness performance of the ensemble optimization based weighting factor-less predictive torque control (w =300r/min， T=0N·m， N=2)
4 论断本文提议了一种基于集成优化的感应电机无权重悉数接洽转矩规则战略。与传统接洽转矩要领比较，该规则要领禁受两个单一规则变量的短处项代替了原有的主张函数，舍弃了权重悉数在不同使命要求下难以调遣的不利影响。此外，两个短处项同期优化，分别中式3个转矩较优与磁链较优的开关现象，并通过集成优化算法，将最优开关现象输出到逆变器中。终末，在2.2kW感应电机平台上考据了该规则算法，对比分析了所提议的规则要领与传统接洽转矩规则在稳态、全转速回转及瞬态的规则后果。实验收场标明，基于集成优化的无权重悉数接洽转矩规则战略具有更好的稳态与动态性能。
参考文件
[1] 席裕庚， 李德伟， 林姝. 模子接洽规则—近况与挑战[J]. 自动化学报， 2013， 39(3): 222-236.
Xi Yugeng， Li Dewei， Lin Shu. Model predictive control-status and challenges[J]. ACTA Automatica Sinica， 2013， 39(3): 222-236.
[2] 郭磊磊， 金楠， 李琰琰. 电压源逆变器编造矢量模子接洽共模电压扼制要领[J]. 电工时代学报， 2020， 35(4): 839-849.
Guo Leilei， Jin Nan， Li Yanyan. Virtual vector based model predictive common-mode voltage reduction method for voltage source inverters[J]. Transactions of China Electrotechnical Society， 2020， 35(4): 839- 849.
[3] 姚骏， 刘瑞阔， 尹潇. 永磁同步电机三矢量低开关频率模子接洽规则究诘[J]. 电工时代学报， 2018， 33(13): 2935-2945.
Yao Jun， Liu Ruikuo， Yin Xiao. Research on 3-vector model predictive control with low switching fre- quency of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society， 2018， 33(13): 2935-2945.
[4] 郑泽东， 王奎， 李永东. 禁受模子接洽规则的交流电机电流规则器[J]. 电工时代学报， 2013， 28(11): 118-123.
Zheng Zedong， Wang Kui， Li Yongdong. Current controller for AC motors using model predictive control[J]. Transactions of China Electrotechnical Society， 2013， 28(11): 118-123.
[5] 杨家强， 黄进. 基于转矩接洽的异步电机平直转矩规则究诘[J]. 浙江大学学报(工学版)， 2005， 39(9): 1277-1281.
Yang Jiaqiang， Huang Jin. Research on direct torque control of induction machine based on torque pre- diction[J]. Journal of Zhejiang University (Engineering Science)， 2005， 39(9): 1277-1281.
[6] 王祯， 尹项根， 陈玉. 基于连结规则集模子接洽规则的MMC桥臂电流规则战略[J]. 电力系统自动化， 2020， 44(10): 85-91.
Wang Zhen， Yin Xianggen， Chen Yu. Arm current control strategy of modular multilevel converter based on continuous control set model predictive control[J]. Automation of Electric Power Systems， 2020， 44(10): 85-91.
[7] 牛里， 杨明， 刘可述. 永磁同步电机电流接洽规则算法[J]. 中国电机工程学报， 2012， 32(6): 131-137.
Niu Li， Yang Ming， Liu Keshu. A predictive current control scheme for permanent magnet synchronous motors[J]. Proceedings of the CSEE， 2012， 32(6): 131-137.
[8] 夏长亮， 王东， 程明. 高遵守电机系统可靠运行与智能规则基础究诘说明[J]. 中国基础科学， 2017， 19(1): 16-23.
Xia Changliang， Wang Dong， Cheng Ming. Advance- ments of basic researches on high-efficiency motor system’s reliability and intelligence control[J]. China Basic Science， 2017， 19(1): 16-23.
[9] 李家祥， 汪凤翔， 柯栋梁. 基于粒子群算法的永磁同步电机模子接洽规则权重悉数想象[J]. 电工时代学报， 2021， 36(1): 50-59.
Li Jiaxiang， Wang Fengxiang， Ke Dongliang. Weightingfactors design of model predictive control for per- manent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Elec- trotechnical Society， 2021， 36(1): 50-59.
[10] 李昱， 郭宏， 平朝春， 等. 基于电流源变流器的永磁同步电机驱动系统全现象变量接洽转矩规则[J]. 电工时代学报， 2021， 36(1): 15-26.
Li Yu， Guo Hong， Ping Zhaochun. A full-state variable predictive torque control of current source converter fed permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society， 2021， 36(1): 15-26.
[11] 赵勇， 黄文新， 林晓刚， 等. 基于权重悉数舍弃和有限规则集优化的双三相永磁容错电机快速接洽平直转矩规则[J]. 电工时代学报， 2021， 36(1): 3-14.
Zhao Yong， Huang Wenxin， Lin Xiaogang. Fast predictive direct torque control of dual three-phase permanent magnet fault tolerant machine based on weighting factor elimination and finite control set optimization[J]. Transactions of China Electrote- chnical Society， 2021， 36(1): 3-14.
[12] 陈文汉， 孙丹， 王铭泽. 断相故障下开绕组永磁同步电机模子接洽规则容错规则战略究诘[J]. 电工时代学报， 2021， 36(1): 77-86.
Chen Wenhan， Sun Dan， Wang Mingze. Research on fault-tolerance strategy based on model predictive control for open-winding PMSM system under open- phase fault[J]. Transactions of China Electrotechnical Society， 2021， 36(1): 77-86.
[13] Li Yu， Zhang Zhenbin， Li Kejun. Predictive current control for voltage source inverters considering dead-time effect[J]. CES Transactions on Electrical Machines and Systems， 2020， 4(1): 35-42.
[14] Bramerdorfer G. Multiobjective electric machine optimization for highest reliability demands[J]. CES Transactions on Electrical Machines and Systems， 2020， 4(2): 71-78.
[15] Rodriguez J， Kazmierkowski M P， Espinoza J R. State of the art of finite control set model predictive control in power electronics[J]. IEEE Transactions on Indu- strial Informatics， 2013， 9(2): 1003-1016.
[16] Karamanakos P， Geyer T. Guidelines for the design of finite control set model predictive controllers[J]. IEEE Transactions on Power Electronics， 2020， 35(7): 7434-7450.
[17] Andersson A， Thiringer T. Assessment of an improved finite control set model predictive current controller for automotive propulsion applications[J]. IEEE Transactions on Industrial Electronics， 2020， 67(1): 91-100.
[18] Vazquez S， Leon J I， Franquelo L G. Model predictive control: a review of its applications in power electronics[J]. IEEE Industrial Electronics Magazine， 2014， 8(1): 16-31.
[19] Hua Wei， Chen Fuyang， Huang Wentao. Multivector- based model predictive control with geometric solution of a five-phase flux-switching permanent magnet motor[J]. IEEE Transactions on Industrial Electronics， 2020， 67(12): 10035-10045.
[20] Wang Fengxiang， Li Shihua， Mei Xuezhu. Model- based predictive direct control strategies for electrical drives: an experimental evaluation of PTC and PCC methods[J]. IEEE Transactions on Industrial Infor- matics， 2015， 11(3): 671-681.
[21] 胡虎， 李永东. 基于区域电压矢量表的交流异步电动机平直转矩接洽规则战略究诘[J]. 电工时代学报， 2004， 19(2): 25-31.
Hu Hu， Li Yongdong. A predictive direct torque control strategies of induction motor based on area voltage vector table[J]. Transactions of China Elec- trotechnical Society， 2004， 19(2): 25-31.
[22] 牛峰， 李奎， 王尧. 永磁同步电机模子接洽平直转矩规则[J]. 电机与规则学报， 2015， 19(12): 60-67.
Niu Feng， Li Kui， Wang Yao. Model predictive direct torque control for permanent magnet synchronous motor[J]. Electric Machines and Control， 2015， 19(12): 60-67.
[23] 夏长亮， 张天一， 周湛清. 结合开关表的三电平逆变器永磁同步电机模子接洽转矩规则[J]. 电工时代学报， 2016， 31(20): 83-92.
Xia Changliang， Zhang Tianyi， Zhou Zhanqing. Model predictive torque control with switching table for neutral point clamped three-level inverter-fed permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society， 2016， 31(20): 83-92.
[24] 张永昌， 杨海涛. 感应电机模子接洽磁链规则[J]. 中国电机工程学报， 2015， 35(3): 719-726.
Zhang Yongchang， Yang Haitao. Model predictive flux control for induction machines[J]. Proceedings of the CSEE， 2015， 35(3): 719-726.
[25] Geyer T. Algebraic tuning guidelines for model predictive torque and flux control[J]. IEEE Transa- ctions on Industry Applications， 2018， 54(5): 4464- 4475.
[26] Dragičević T， Novak M. Weighting factor design in model predictive control of power electronic con- verters: an artificial neural network approach[J]. IEEE Transactions on Industrial Electronics， 2019， 66(11): 8870-8880.
[27] Norambuena M， Rodriguez J， Zhang Zhenbin. A very simple strategy for high-quality performance of AC machines using model predictive control[J]. IEEE Transactions on Power Electronics， 2019， 34(1): 794-800.
[28] 魏玉春， 夏长亮， 刘涛. 两电机转矩同步系统有限集模子接洽规则[J]. 电工时代学报， 2016， 31(19): 115-122.
Wei Yuchun， Xia Changliang， Liu Tao. Finite control set model predictive control for dual-motor torque synchronous system[J]. Transactions of China Elec- trotechnical Society， 2016， 31(19): 115-122.
[29] 徐艳平， 李园园， 张保程. 一种舍弃权重悉数三矢量模子接洽转矩规则[J]. 电工时代学报， 2018， 33(16): 3925-3934.
Xu Yanping， Li Yuanyuan， Zhang Baocheng. Three- vector based model predictive torque control of eliminating weighting factor[J]. Transactions of China Electrotechnical Society， 2018， 33(16): 3925- 3934.
[30] 张敏敏， 李宏光， 宿翀. 基于模子接洽规则的动态多属性决议要领[J]. 规则工程， 2018， 25(3): 535-540.
Zhang Minmin， Li Hongguang， Su Chong. A model predictive control based approach for dynamic multi- attribute decision making[J]. Control Engineering of China， 2018， 25(3): 535-540.
[31] Rojas C， Rodriguez J， Villarroel F. Predictive torque and flux control without weighting factors[J]. IEEE Transactions on Industrial Electronics， 2013， 60(2): 681-690.
[32] Zhang Yongchang， Bai Yuning， Yang Haitao. A universal multiple-vector-based model predictive control of induction motor drives[J]. IEEE Transa- ctions on Power Electronics， 2018， 33(8): 6957-6969.
Ensemble Optimization Based Weighting Factor-Less Predictive Torque Control for Induction Machines
Abstract As an emerging control strategy， predictive torque control (PTC) selects the optimal switching state by calculating the torque and flux tracking errors in the objective function， which is widely spread in the AC electrical drive system. Compared with traditional field orient control (FOC)， PTC shows its superiority of fast dynamic response and low switching frequency. In order to unify the different terms in the objective function， parameter design is required to modify the weighting of torque and flux. However， the empirical weighting parameter is not easy to be fine-tuned according to different operating conditions. To solve the aforementioned issue， an ensemble optimization based weighting factor-less PTC is proposed for induction machines. The proposed method optimizes the tracking errors of torque and flux simultaneously. Thus， three switching states for optimal torque and flux are obtained， respectively. The optimal solution is subsequently achieved by the ensemble optimization mechanism. The effectiveness of the proposed method is verified by experimental results. Compared with the conventional PTC， the proposed method performs better at both steady state and transient state.
keywords：Induction machines， predictive torque control， weighting factor-less， ensemble optimization
DOI: 10.19595/j.cnki.1000-6753.tces.201587
中图分类号：TM346
谢昊天 男，1990年生，博士究诘生，究诘所在为电机驱动系统的模子接洽规则、无位置传感器规则时代。E-mail: haotian.xie@tum.de
汪凤翔 男，1982年生，究诘员，博士生导师，究诘所在为电机驱动系统及电力电子变换器的模子接洽规则、无位置传感器规则时代。E-mail: fengxiang.wang@fjirsm.ac.cn（通讯作家）
收稿日历 2020-12-04
改稿日历 2021-01-21
国度天然科学基金资助样式（51877207）。
（裁剪 崔爱静）黄色小电影